鹿児島現代物理勉強会

物理理論 (物理理論・科学史の解説を記載してあります) 順次更新中
(用語をクリックすると解説ファイルにリンクするところもあります。)
(中・高レベルから大学・社会人まで)
☆物理用語の解説です。 (ほぼ成立順に列記してあります。)
1.古典力学
19世紀末頃まではニュートン力学と電磁気学を用いると全ての物理現象が説明できると信じられていた。
現在でもわたしたちの身のまわりで起こる人の目で直接観察できるような物理現象で、光の速さに近いところで
おこる現象や極微の世界以外においては、古典理論は十分有効である。
Ⅰ.ニュートン力学(1687年) 〜低エネルギー、低速における物理現象では現在でも
十分に使える物理法則
惑星の運動などもかなりの精密さで運動を記述できる。
ニュートンの運動の3法則 →高等学校物理・物理基礎などにて学習する。
①慣性の法則 → 力がはたらかないか合力が0のときに、物体は等速直線運動を続ける。
慣性の法則が成り立つ慣性系が存在することを明示する。
②運動の法則 →
③作用反作用の法則 → 力が物体から他の物体に働く(作用)と物体には他の物体から物体へ
同じ作用線上で反対向きに同じ大きさの力が働く(反作用)。
我々の身の回りで起こるごく普通の物体の運動は、この三法則で説明ができる。
☆運動量・力積・エネルギー
★回転座標系 〜 回転する立場での運動の記述(遠心力・コリオリの力など見かけの力が現れる)
★剛体の運動 〜 力を受けても変形しない理想的な物体系(剛体)の運動
★剛体の運動その2(オイラーの運動方程式)
◆「オイラーディスクの運動」の動画。
★解析力学 〜任意の座標変数で物体の運動を自由に取り扱える。
ラグラジアン・ハミルトニアン
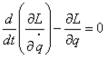
<Key point>
任意の座標系で一般的に物理法則を取り扱えるように成熟したことが後に量子力学の発展
につながっていく。解析力学に習熟することが現代物理の理解への第一歩にもなる。
変分原理 → 最速降下曲線(京大院試問題)
最小作用の原理 → 一般的な運動方程式の導出
Ⅱ.物理数学 →物理現象を量的に表すのに欠かせない数学。大学の1・2年生で学習します。
ベクトル表記が大活躍します。
◆微分積分 〜物体の速度・加速度・位置などの時間的変化を精密に計算することを
目的に発展した数学。
高校数学では1変数しか扱わないが、より一般的な物理を扱うには2変数以上を
扱う偏微分や重積分に発展します。
◆ベクトル解析 〜ベクトルを用いて電磁場や物体の運動を記述するのには欠かせない。
高校の物理が数学的にしっかりと扱えるようになります。
「ベクトル入門」(パワーポイント)
①勾配 〜 ポテンシャルの変化から電場や重力場を求める。
②曲率 〜 ある曲線が空間中でどう曲がっているかを示す値。
③曲線座標系 〜デカルト座標系以外の任意の変数を用いてベクトルを扱う。
④直交座標系 〜基底ベクトルがお互い垂直である。
◆線形代数 〜 行列を用いての数の表現。量子力学の記述・理解には欠かせない。
ハイゼンベルク形式
Ⅲ.電磁気学 〜 ガウスの法則 アンペールの法則 ビオ・サバールの法則
マックスウェルの電磁方程式(1864年) → 電磁気に関する物理法則を数学的 に方程式として
定式化した。 光速Cが、方程式中に含まれる。
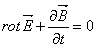
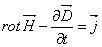
◎ベクトル解析と電磁気学(パワーポイント)
→ 電磁気学を数学的に取り扱うのにベクトル解析が一番便利である。
★電磁波の伝わり方
★電磁波の放射
★ベクトルポテンシャル
★ポテンシャル方程式
★遅延ポテンシャル
★マックスウェルの電磁方程式(テンソル形式表示)
Ⅳ.熱力学
①マクスウェルの関係式
Ⅴ.流体力学 〜 流体(気体・液体)の運動やその中での物体の運動に関する力学
ボールがカーブする(変化球)、航空機が飛行できることなどを説明する。
2.特殊相対性理論(1905年)(アインシュタイン)
※高校で学習する数学の範囲内で理解可能な理論です。
数Ⅲまで学習を終えた人は数式の展開を示してありますのでチャレンジしてください。
Ⅰ.マイケルソン・モーリーの実験(1887年)→ 光速は、どの慣性系から観測しても同じである。
光速不変の原理
Ⅱ.特殊相対性理論の構築
①光速不変の原理
②慣性系はお互いに同等である。 → この2点①②を基本原理とする。
☆どの慣性系でも時間は一様に流れるであろうとする常識概念が初めて打ち破られる。
Ⅲ.ローレンツ変換 (各慣性系の座標間の変換公式)
★ローレンツ変換導出過程
ニュートン力学は、光速に近くなると、ローレンツ変換をしても運動方程式の形式が変化しないように
(共変性を持つように)修正される。
「ローレンツ変換のエクセルVBAソフト」 → ローレンツ変換の様子が数値で確認できるソフトです。
↓
特殊相対性理論(パワーポイント)
◎特殊相対性理論についての全体的な概要を説明したシートです。
1 |
相対論的運動方程式 |
2 |
四元運動量の性質(ローレンツスカラー量) |
3 |
速度の合成 |
4 |
マックスウェル方程式のローレンツ変換 |
5 |
特殊相対論的効果による近日点移動 |
時間と空間は同等の概念である。(時空間)
質量とエネルギーは等価
◆現代物理に用いられる数学(物理数学)について ①現代物理の数学的準備事項Ⅰ ②グリーン関数について ③δ関数の活用 ④フーリエ級数 ⑤複素関数 |
◆物理のキーポイント その1 ★ローレンツ変換を施したときに、物理法則の形式が変化しない! ↓ ローレンツ対称性 ●特殊相対性理論は、慣性系においてはローレンツ対称性をもつ! ●マクスウェルの電磁方程式もローレンツ対称性をもっていた! |
3.一般相対性理論(1915年)(アインシュタイン)
加速度系まで含むすべての座標系において物理法則は同等である。
重力と加速度座標系で生じる力は区別がつかない。→ 等価原理
※局所的に慣性系を作り出すことができる。
★計量テンソル初歩 → 空間の曲がり具合を表す量
質量のある物体のまわりの空間は曲げられる。 → 重力レンズ
4.量子力学→ 電子などの微視的な粒子の運動をミクロな立場で記述することのできる物理法則
★ラザフォード散乱実験 → ラザフォードの原子模型(1911年)
★ボーアの原子模型
★不確定性原理(ハイゼンベルク)(1927年)→ 電子の位置と運動量は同時に正確に決めることはできない。
必ず位置か運動量のどちらかに不確定さが残る。
●<だいたいここまでは、高校物理で微分積分を用いずに学習する>
★<解析力学・一般相対論については全く学習しない。>
★量子力学概要(パワーポイント)→ 量子力学の概要が説明してあります。
①行列力学(ハイゼンベルグ)(1925年)
②シュレディンガー方程式(シュレディンガー)(1926年)
※非相対論的な方程式 ψは波動関数を意味しその二乗は粒子の存在確率を示す。
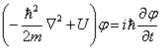
①と②は数学的に同等の概念
★量子力学での演算子の扱い方(パワーポイント)
★一般化角運動量(交換関係を用いた一般的な取り扱い・スピンも取り扱う)
Ⅰ.相対論的量子力学(1928年)〜相対論と量子力学の初めての合体 ・量子力学に特殊相対論を組み入れた理論。 量子力学の方程式がローレンツ対称性を持つようにディラックが定式化。 正と負のエネルギー解が導れる。 電子が負のエネルギー持って運動するとはどういうこと? 負のエネルギー解は、正のエネルギーを持つ陽電子(反粒子)の波動関数の解である と解釈された。 電子の運動は、4個の一次独立な波動関数(スピノル)の線形結合で表現される。 また、ディラック方程式により、スピンが自動的に導かれこともわかった。 反物質は、物質の持つ電荷の符号が反対である以外はすべての物理的性質が同じで ある。 ディラック(Dirac)の信念  ●物理法則は美しくなければならない! ●量子力学もローレンツ対称性を持つはずだ! ↓ 理論から逆に実験事実を導けた(スピン・陽電子)! ↓ ★対称性は物理法則作りの指導原理としての地位を確立していく。 Ⅱ.対称性 ①回転対称性 ②並進対称性 ③ローレンツ対称性 物理法則が①〜③の対称性を持つときにそれぞれ保存量が導かれる。 ★詳細は → 物理と対称性(パワーポイント) |
★粒子分布関数
フェルミ粒子 → パウリの排他原理 フェルミディラック統計
ボーズ粒子 ボーズ・アインシュタイン統計
原子核内部の核子間で働く力の理解(核力について)
★中間子理論(湯川秀樹)(1935年) → 日本人初のノーベル賞受賞(1949年)
原子核中の核子は中間子を交換することで結合している。 核力(強い力)
力は粒子を交換することではたらくというアイデア
◆物理学者の負の歴史 純粋な物理学の探求は一旦停止◆ ルーズベルト大統領に原爆製造を書簡により具申(アインシュタイン)(1939年) アメリカ マンハッタン計画・ロスアラモス研究所開設(1943年)所長(オッペンハイマー) 1万人以上を動員 原子爆弾の完成(1945年7月) → 広島・長崎に投下(同8月) 日本 二号研究(陸軍・理研)・F研究(海軍・京大)として研究したが途中で断念 戦後、理研の加速器は米軍により東京湾に投棄される。 日本の原爆研究を調査した米軍の報告書によると、日本の研究段階はまだ 基礎的段階に止まっており、米国の1942年の段階に相当すると結論づけた。 科学者の人類に対する社会的責任を考えさせる歴史でもある。 |
★<これ以降は、物理学系の大学院で学習する>
5.場の量子論(古川先生の県民大学講座は主にこれ以降)
☆高エネルギー状態においても成り立つ究極の量子力学。粒子の生成消滅を扱う。
●基本となるのは粒子ではなく「場」
●場の性質 → 物理法則を決める。素粒子物理学は、場の量子論の枠組みで記述。
●粒子 → 場にエネルギーが局在化している状態。
「力はゲージ粒子の交換で生じる」という考え方.
三つの力「電磁力」「弱い力」「強い力」を統一的に表現する場の量子論 → 「ゲージ理論」
実験的に検証されたゲージ理論の模型 → 「標準模型」(スタンダード モデル)
<ゲージ理論について> ★ゲージ理論の展開
| ゲージ変換 → 理論に現れる粒子の自由度に対して、位相と呼ばれる量を時空の位置に依存させて 変換すること ゲージ対称性〜 ゲージ変換に対する不変性(ゲージ不変性について) ゲージ理論 〜 ゲージ対称性を持つ理論 ゲージ場 〜 ゲージ対称性を持たせるのに導入される粒子 4次元時空全ての点で一斉に行う変換 → 大域的(グローバル)変換 〃 の局所的なところで行う変換 → 局所的(ローカル)変換 ゲージ理論の展開の流れ ★電磁相互作用の場合 ①ローカルゲージ対称性を物理の指導原理と見なす ②自由場のディラック・ラグラジアンは、ローカルゲージ対称性を持たない ↓ ③新たな「場」・「ゲージ場」を導入してラグラジアンを変更 ④ローカルゲージ変換後のラグラジアンが不変となる。 ⑤ローカルゲージ対称性 → 電子と相互作用するゲージ粒子(フォトン・光子)が導かれる。 電子とフォトンの結合の強さ → ーq=e ゲージ理論の学習帳(作成途上・パワーポイント) ゲージ理論についての個人的な学習帳です。 |
↓
| 量子電磁力学(QED) → 荷電粒子間の電磁相互作用を量子論的に記述する 場の量子論 光子が電磁気力を媒介する。 ☆量子電磁気学(QED)の式の導出を解説してあります。 電弱統一理論(ワインバーグ・サラム理論) → SU(2)×U(1)と呼ばれる群のゲージ理論 電磁気力・弱い力を扱う場の量子論 量子色力学(QCD) → SU(3)と呼ばれる群のゲージ理論 強い相互作用を扱う場の量子論 群論とは → かけ算の定義されている集合のこと 群に含まれる要素は一般に行列を用いて表せる。 U(n) → n行n列の正方行列でその行列の複素転置共役が逆行列となる行列 U(1) 1行一列のユニタリー行列 複素数とその複素共役との積が1になる量 SU(2) 2行2列の行列で行列式が1であるユニタリー行列 SU(3) 3行3列の行列で行列式が 〃 |
くりこみ理論(朝永振一郎)(1948〜1949年) → 日本人二人目のノーベル賞受賞(1965年)
電子陽子深非弾性散乱 → 陽子に電子を衝突させて、電子の散乱される様子を観測
電子が大きな角度で散乱された
↓
陽子のパートン構造の確立
↓
陽子中の核となるものの存在を示唆)(1969年)
クォーク模型(1964年) →
☆高校物理でも扱います。
ハドロン → 強い相互作用で結合している複合粒子 〜 クォークとグルーオンで構成
種類①バリオン(重粒子) 〜 陽子・中性子(3個のクォークで構成)
②メソン(中間子) 〜 (クォークと反クォークの2個で構成)
レプトン
自発的対称性の破れ(南部)
CP対称性の破れ(益川・小林) → KEKのベル実験装置にて実験的に確認(2001年)
ノーベル物理学賞受賞(2008年) B中間子と反B中間子の崩壊が少し異なる。
粒子と反粒子の従う物理法則が少し異なり、ビッグバンにおいて
は同数存在したが、結果的に反粒子の方が先になくなり現在
は物質粒子で構成される。

ベル装置の粒子の衝突点付近 KEK HPより
ヒッグス理論(ヒッグス)(1964年)
ヒッグス粒子 → LHCにて確認(2013年)
標準理論・標準模型 → ヒッグス粒子の確認により理論的に確定
確定はしたが、宇宙の中で物質の占める割合は4〜5%
ダークマター → 電磁気力の影響を受けず観測不能。質量を持ち他の物質との
重力相互作用は行う。
ダークエネルギー → 宇宙を膨張させるエネルギー
宇宙の終焉 ビッグリップ
ビッグクランチ
6.超弦理論
素粒子は点ではなく、ひも(弦)で扱える。
7.宇宙論
宇宙の始まりと未来(パワーポイント)
ビッグバン理論 → 宇宙は一点の火の玉の状態から始まりそのエネルギーの中から物質粒子が
創世され現在に至る。
インフレーション理論(佐藤勝彦) 〜 ビッグバンの前に宇宙は指数関数的に膨張.
マルチバース宇宙論
人間原理
| ●素粒子の話(KEKキッズサイエンティスト) キッズといいながらかなり詳しい。(外部リンク) ●英語の達者な人はこちらもどうぞ Particle Adventure |
8.現代物理学の応用
①量子コンピュータ入門
②医学への応用
・PET診断 〜 陽電子放出核種を用いて、ガン細胞の場所等を特定する診断方法
・粒子線治療 〜 陽子・炭素原子核などの粒子線を用いて放射線治療を行う。
・医学物理士 〜 放射線治療等の医療分野において、物理学の専門的知識をもって治療計画
等の支援等を行う。
その他